floating point 직관적 이해
컴퓨터에서 실수(부동형소수점, floating point)가 어떻게 표현되는지 알아보자.
1. 핵심요약
- sign bit, range bits, offset bits 로 실수 표현
- 값이 양수인지 음수인지 결정 (sign bit, 1)
- 나타내려는 값의 범위를 정의 (range bits 사용, 8)
- 정의된 범위 안에서 값을 선택 (offset bits 사용, 23)
- 실수에 저장하는 값이 커질수록, 나타내는 값의 정확도가 떨어짐
2. 실수 표현의 이해
컴퓨터에서 실수를 표현하기 위해서 {Wikipedia} IEEE754 표준을 사용한다고 한다. 유효숫자, 지수부, 가수부 등으로 설명을 하는데 이해가 쉽지는 않다.
{책} 셰이더 코딩 입문 / 카일 할러데이 / 조형재 역 / 2019.11.29 책에서의 설명이 실수의 표현을 직관적으로 이해하는 데 좋아 보여서, 정리해 두려 한다.
보통 4bytes(32bits) 로 실수를 표현한다.
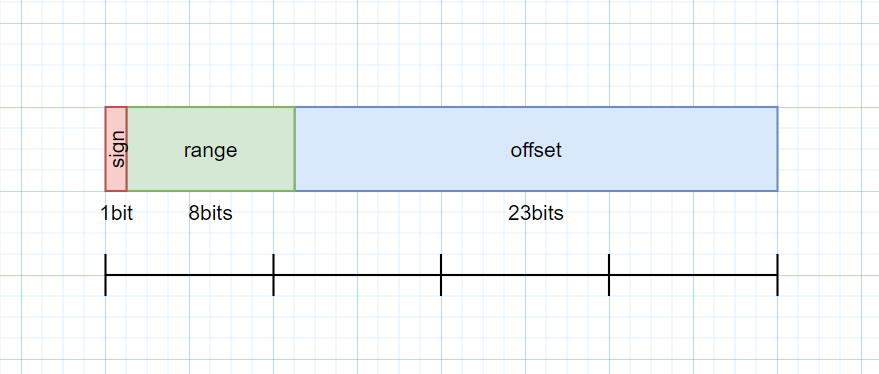
위의 그림처럼 메모리를 세부분을 나눠서 표현한다.
첫 비트는 부호(sign) 비트
그 다음 8개 비트는 보통 지수(exponent)비트라고 하는데, 여기서는 범위(range) 비트라고 한다.
마지막 23비트는 보통 가수(mantissa) 라고 하는데, 여기서는 오프셋(offset) 비트라고 한다.
실수 하나를 표현하는 과정은 큰 틀에서 아래와 같다.
- 값이 양수인지 음수인지 결정 (sign bit)
- 나타내려는 값의 범위를 정의 (range bits 사용)
- 정의된 범위 안에서 값을 선택 (offset bits 사용)
간략화한 예시로 각 단계별로 따라가 보자.
2.1. 예시 #1
2.5를 나타내고 싶다고 해보자. 단, 간략화해서 offset bit 부분을 위해 2비트만 쓸 수 있다고 해보자.
🔷 sign bit
먼저 양수니까, sign bit 는 0으로 둔다. (0이 양수, 1이 음수)
🔷 range bits
이제, 값의 범위를 정해야 하는데, 2의 지수승에서 나타내려는 숫자보다는 작으면서 가장 가까운 숫자를 찾는다. 여기서는 $2^{\textcolor{magenta}{1}}$ , 즉, 2를 선택하면 되겠다.
선택한 숫자 ${\textcolor{magenta}{1}}$이 우리가 의미적으로 의도한 정수 이다. 이 값을 통해 우리가 표현할 수 있는 범위(range)가 정해진다.
여기서는 $2^{\textcolor{magenta}{1}}$이 범위의 시작이 되고, 그 다음 숫자의 지수승, $2^{\textcolor{magenta}{1}+1}$ 까지가 우리의 범위가 된다.
- range 시작: $2^{\textcolor{magenta}{1}}$
- range 길이: $2^{\textcolor{magenta}{1}+1} - 2^{\textcolor{magenta}{1}} = \textcolor{red}{2}$
다시 말하면, 의도한 정수 하나를 선택함으로써, range의 시작 값이 정해지고, range의 길이도 같이 정해진다.
단, 마지막 값은 포함하지 않는다.
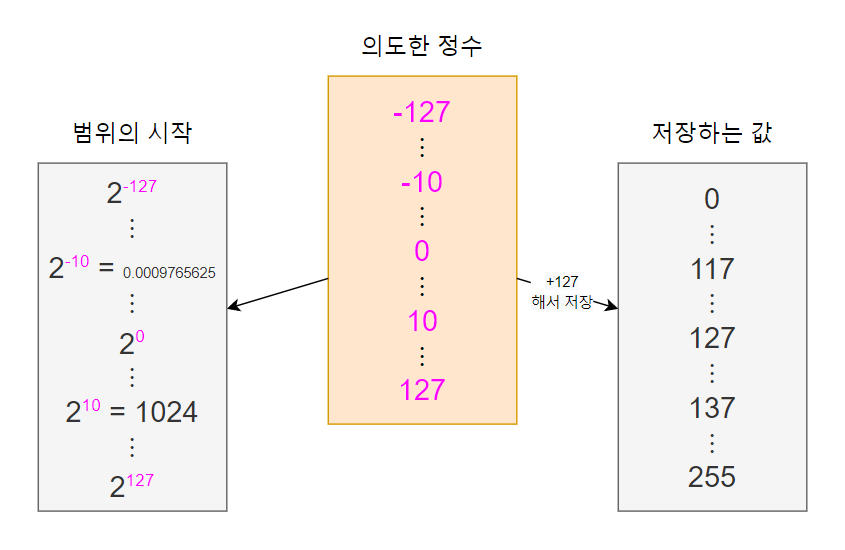
그리고 실제 range bits 영역에 저장하는 값은 +127한 값을 이진수로 저장한다.
🔷 offset bits
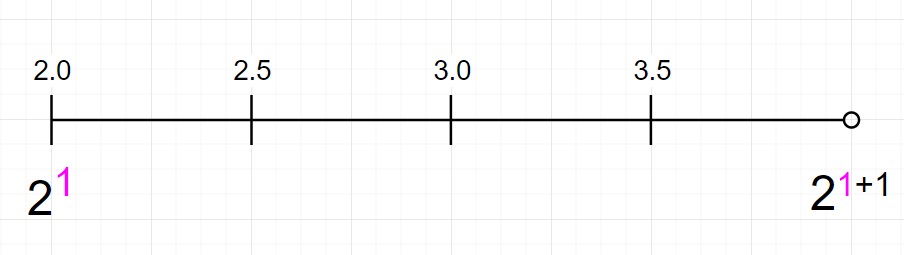
이제 정해진 범위 안에 offset bit로 표현할 수 있는 개수 만큼 눈금으로 표시한다.
2비트만 쓴다고 했으므로, 총 $2^2={\textcolor{orange}{4}}$개의 오프셋을 표현할 수 있다.
offset 이 0, 1, 2, 3 이면 각각 2.0, 2.5, 3.0, 3.5가 되는 것이다.
| 값 | 계산 |
|---|---|
| 2 | $\Large 2^{\textcolor{magenta}{1}} + (\frac{0}{\textcolor{orange}{4}} \times \textcolor{red}{2})$ |
| 2.5 | $\Large 2^{\textcolor{magenta}{1}} + (\frac{1}{\textcolor{orange}{4}} \times \textcolor{red}{2})$ |
| 3.0 | $\Large 2^{\textcolor{magenta}{1}} + (\frac{2}{\textcolor{orange}{4}} \times \textcolor{red}{2})$ |
| 2.5 | $\Large 2^{\textcolor{magenta}{1}} + (\frac{3}{\textcolor{orange}{4}} \times \textcolor{red}{2})$ |
일반화 해보면 아래 정도로 표현할 수 있겠다.
값 =
range 시작값+ (offset/눈금수) * (range 길이)
즉, sign bit 0, range bits 128(의도한 정수1), offset bits 1이면 2.5를 의미하게 된다.
2.2. 예시 #2
🔷 range bits
의도한 정수가 10 이라면…
- 실제 저장하는 값 : 138 (의도한 정수에 127을 더해서 저장한다고 생각)
- range 시작값 : $2^{\textcolor{magenta}{10}} = 1024$
- range 끝(미포함) : $2^{{\textcolor{magenta}{10}}+1} = 2048$
- range 길이 : $2^{{\textcolor{magenta}{10}}+1} - 2^{\textcolor{magenta}{10}} = \textcolor{red}{1024}$
🔷 offset bits
offset bits 에 할당된 영역이 2비트 라면…
- 눈금수 : $\textcolor{orange}{4}$
| 값 | 계산 |
|---|---|
| 1024 | $\Large 2^{\textcolor{magenta}{10}} + (\frac{0}{\textcolor{orange}{4}} \times \textcolor{red}{1024})$ |
| 1280 | $\Large 2^{\textcolor{magenta}{10}} + (\frac{1}{\textcolor{orange}{4}} \times \textcolor{red}{1024})$ |
| 1536 | $\Large 2^{\textcolor{magenta}{10}} + (\frac{2}{\textcolor{orange}{4}} \times \textcolor{red}{1024})$ |
| 1792 | $\Large 2^{\textcolor{magenta}{10}} + (\frac{3}{\textcolor{orange}{4}} \times \textcolor{red}{1024})$ |
이 상황에서 offset bits 영역이 2비트 밖에 없는 관계로, 중간의 값들은 위 표에서 가까운 값에 맞춰지게 된다.
오직 네 개의 값으로는 정확한 값을 표현하기 어렵다.
그런데, 예시 #1 보다 여기에서 정확도 문제가 두드러져 보인다. range 길이가 훨씬 커졌는데, 나누는 눈금 수는 같기 때문이다.
실수에 저장하는 값이 커질수록, 나타내는 값의 정확도가 떨어짐
2.2. 예시 #3
이제 실제 32비트 상황을 살펴보자. (offset bits 영역으로 23bits 사용)
🔷 range bits 의도한 정수가 1이라면…
- 실제 저장하는 값 : 128 (의도한 정수에 127을 더해서 저장한다고 생각)
- range 시작값 : $2^{\textcolor{magenta}{1}} = 2$
- range 끝(미포함) : $2^{{\textcolor{magenta}{1}}+1} = 4$
- range 길이 : $2^{{\textcolor{magenta}{1}}+1} - 2^{\textcolor{magenta}{1}} = \textcolor{red}{2}$
🔷 offset bits
offset bits 에 할당된 영역이 23비트…
- 눈금수: $2^{23} = {\textcolor{orange}{8388608}}$
| 값 | 계산 |
|---|---|
| 2 | $\Large 2^{\textcolor{magenta}{1}} + (\frac{0}{\textcolor{orange}{8388608}} \times \textcolor{red}{2})$ |
| 2.00000023842 | $\Large 2^{\textcolor{magenta}{1}} + (\frac{1}{\textcolor{orange}{8388608}} \times \textcolor{red}{2})$ |
| 2.00000047684 | $\Large 2^{\textcolor{magenta}{1}} + (\frac{3}{\textcolor{orange}{8388608}} \times \textcolor{red}{2})$ |
| 2.00000071526 | $\Large 2^{\textcolor{magenta}{1}} + (\frac{4}{\textcolor{orange}{8388608}} \times \textcolor{red}{2})$ |
| … | … |
23비트를 오프셋 비트로 사용하더라도, 여전히 한계는 있다. 예를 들어 2.0000003 같은 수를 정확히 나타낼 수 없다.