'Euler Angles & Homogeneous Coordinates - Vulkan Game Engine Tutorial 12' 정리

LittleVulkanEngine 을 따라 만들어 보면서, Vulkan을 배워봅시다.

1. 주요내용

• Transformation matrix 에 이동도 포함 (Homogeneous Coodinates 이용)
• 3차원에서 회전 설명
• 모델을 3차원의 큐브로 변경

2. 이론 설명

2.1. translation 표현

29s

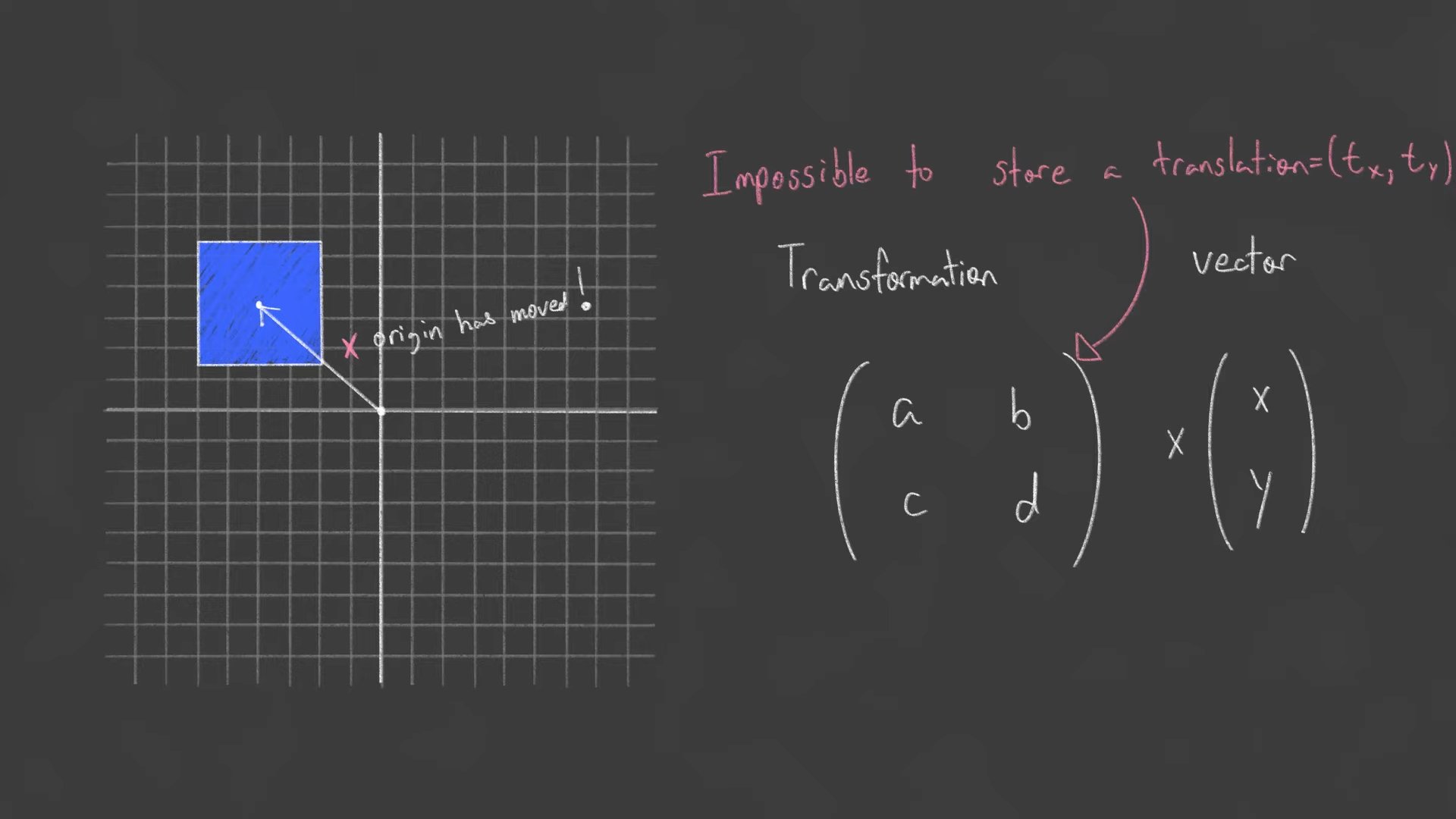
2x2 매트릭스로는 translation 까지 나타낼 수 없었습니다.

111s

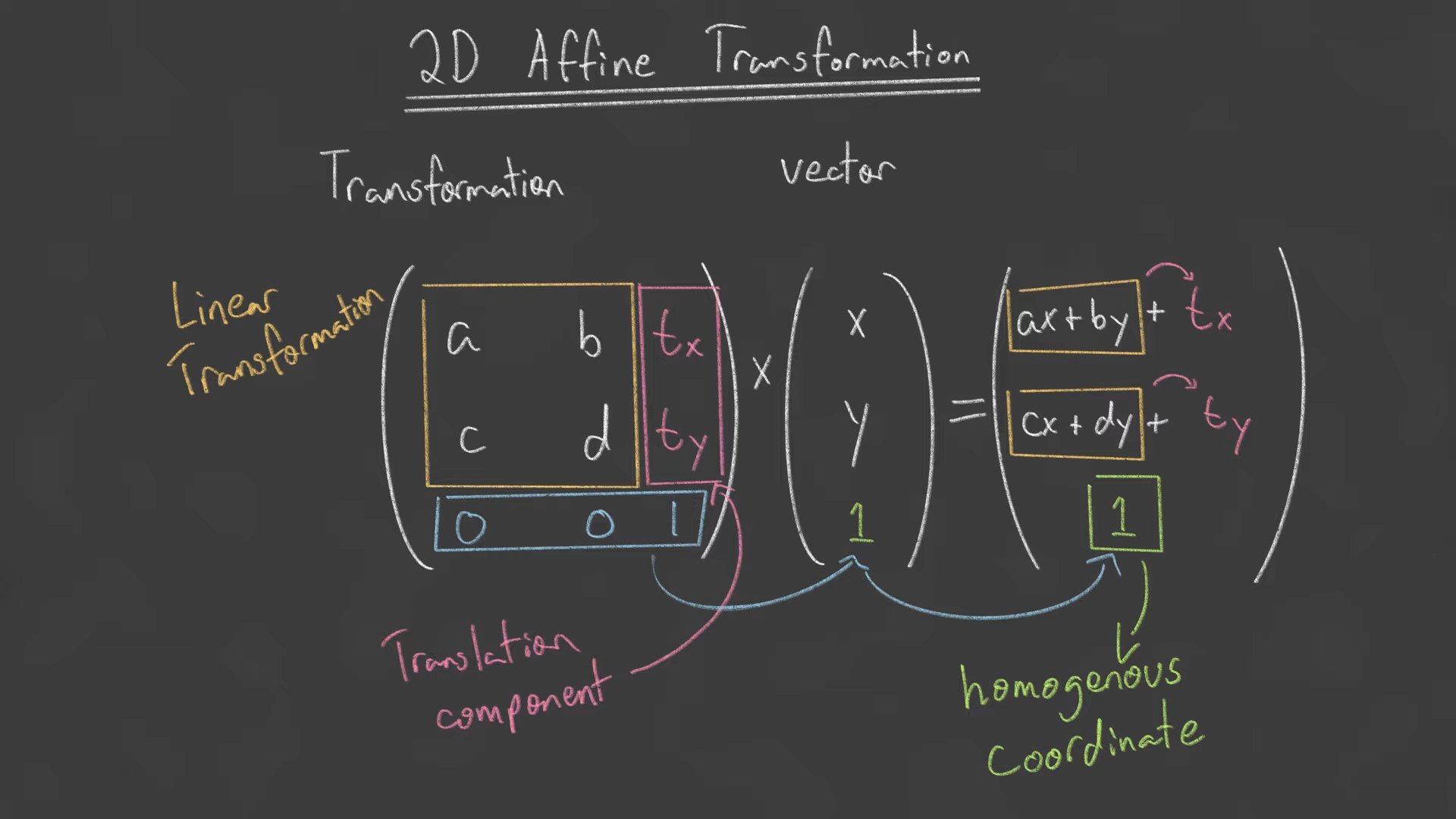
요렇게 대상 점 (x, y) 에 1을 추가하고, 원래 매트릭스를 위와 같이 3x3으로 만들면, 이동까지 나타낼 수 있습니다. 1을 추가한 벡터를 homogeneous coodinate 라고 말하는 것 같습니다.

144s

이제 매트릭를 잘 곱해서 요런 것도 할 수 있습니다. (원점이 아니라 특정 점을 기준으로 회전) 회전 축이 될 특정 점을 원점으로 이동시키고(T1), 회전을 한 뒤(Rotate), 위치 옮겼던 만큼 다시 옮기면(T2) 됩니다. 오른쪽부터 하니까 T = T2 * R * T1 이 되지요.

2.2. 점이 아닌 벡터의 경우

벡터는 크기와 방향만 있으므로, 위치 이동은 의미가 없습니다.

219s

대상 벡터 (x, y) 를 (x, y, 0) 으로 나타내면 원하는 대로 변환이 됩니다.

237s

즉, 점은 마지막 컴포넌트에 1을 넣고, 벡터는 0을 넣어 사용합니다.

2.3. 3차원에 적용

268s

2차원에서 3차원로 갈 때, 생긴 모양은 특별할 건 없습니다.

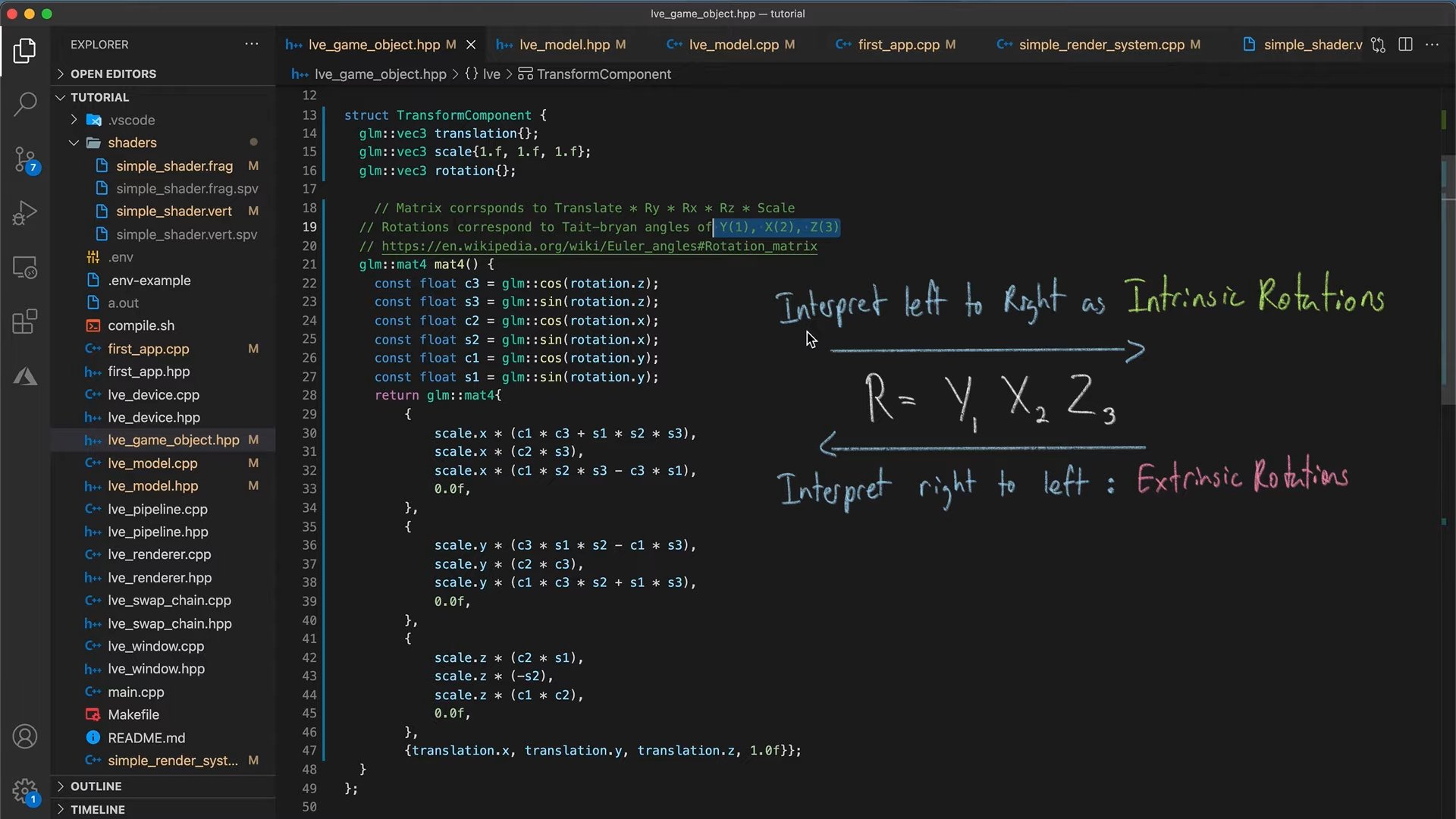
다만 회전을 나타내는 게 조금 복잡해 집니다. 여러 방식이 있는데, 우리는 각 축별로 회전시키는 Euler angles 방식을 따를 겁니다. 각 축별 회전 시키는 각도에 따라, sin, cos 값을 계산해서 적절히 곱하고 더하고 하네요. 그런가 부다 합시다 ㅠㅜ

2.4. intrinsic vs extrinsic rotation

intrinsic rotation은 회전할 때 축도 같이 회전하고(local 좌표계), extrinsic 은 축은 그대로 있습니다. (global 좌표계) 고거에 따라서 회전을 왼쪽부터 혹은 오른쪽 부터 해석하면 된다고 합니다. 일단 그런게 있구나 하겠습니다. ㅠㅜ

3. 코드 수정

3.1. LveModel 클래스 수정

• 3차원을 표현할 수 있도록 Vertex 구조체의 position 타입 변경

3.2. FirstApp 클래스 수정

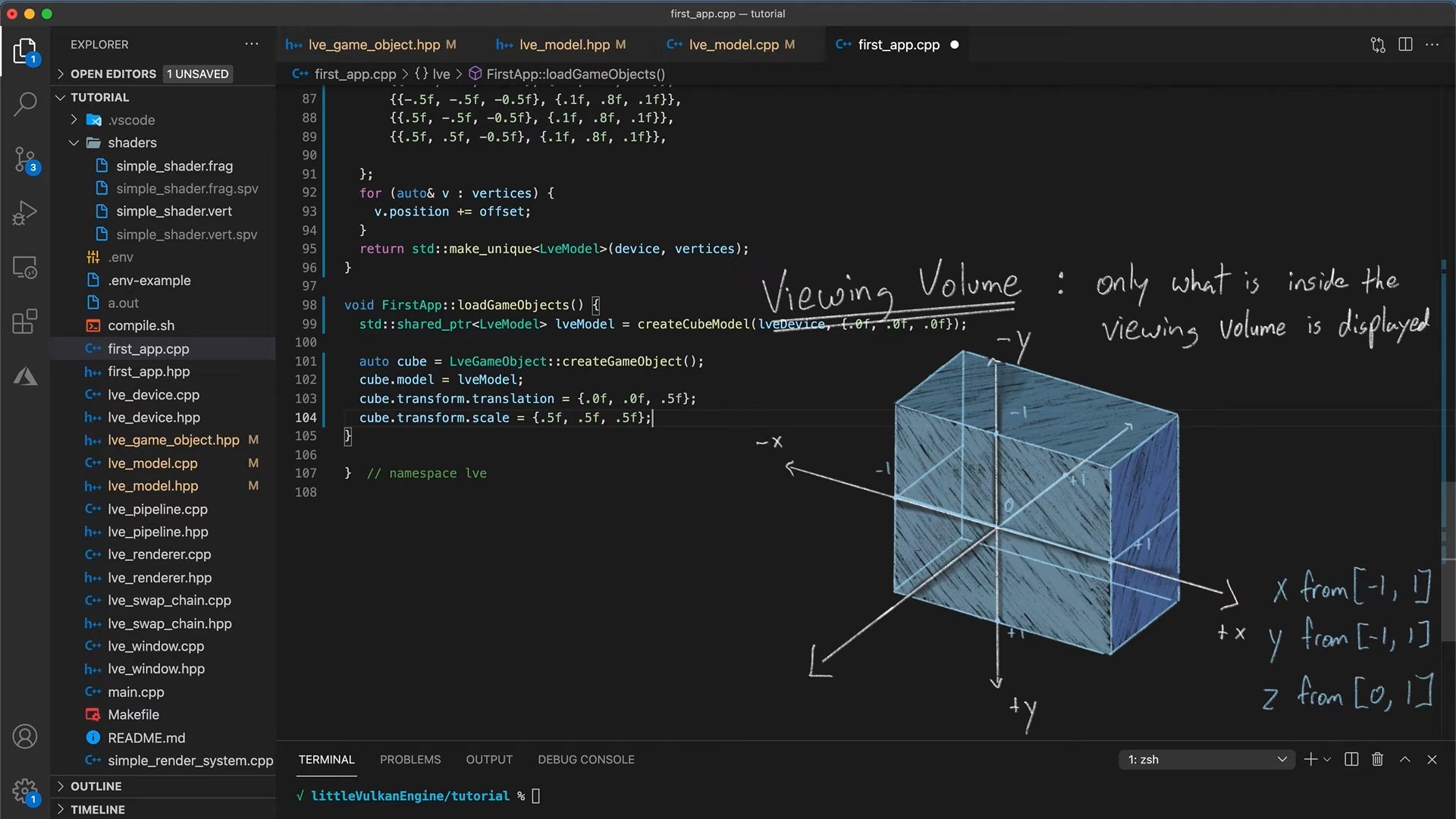
• loadGameObjects() 에서 큐브 모델 만들어서 사용
• 위치랑 스케일 살짝 조정

769s

영역 안에 들어가게 할려고 scale 살짝 줄였습ㄴ디ㅏ.

3.3. GameObject 클래스 수정

• TransformComponent 이름 변경
• 3차원 표현을 위한 변수 타입 변경
• transformation matrix 를 위해 4x4 매트릭스를 리턴하는 mat4() 구현

3.4. SimpleRenderSystem 클래스 수정

• renderGameObjects() 에서 애니메니션을 위해서 GameOjbect의 회전 값 변경후, mat4() 호출해서 transform 준비

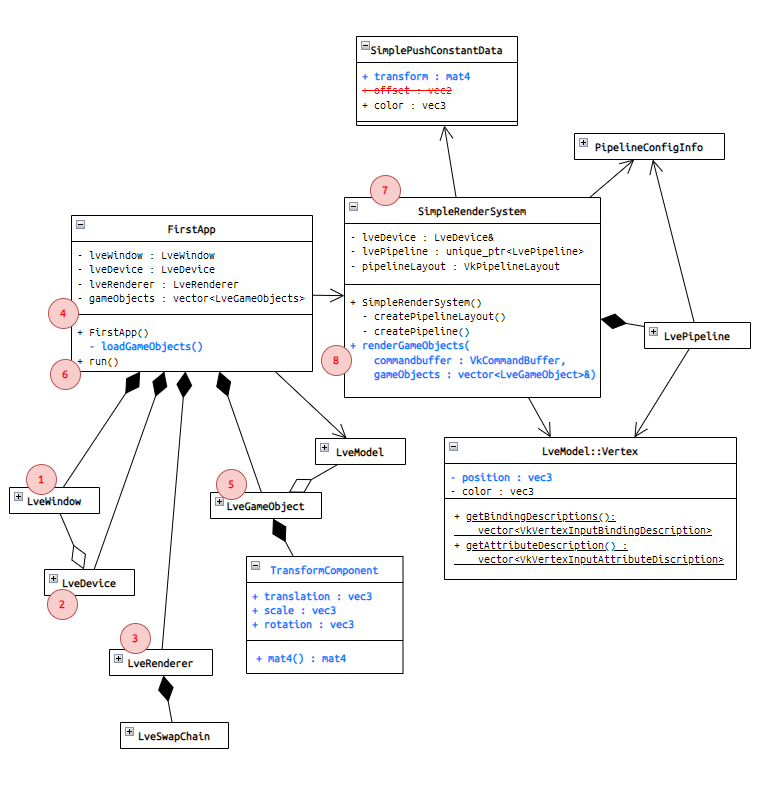
3.5. 다이어그램

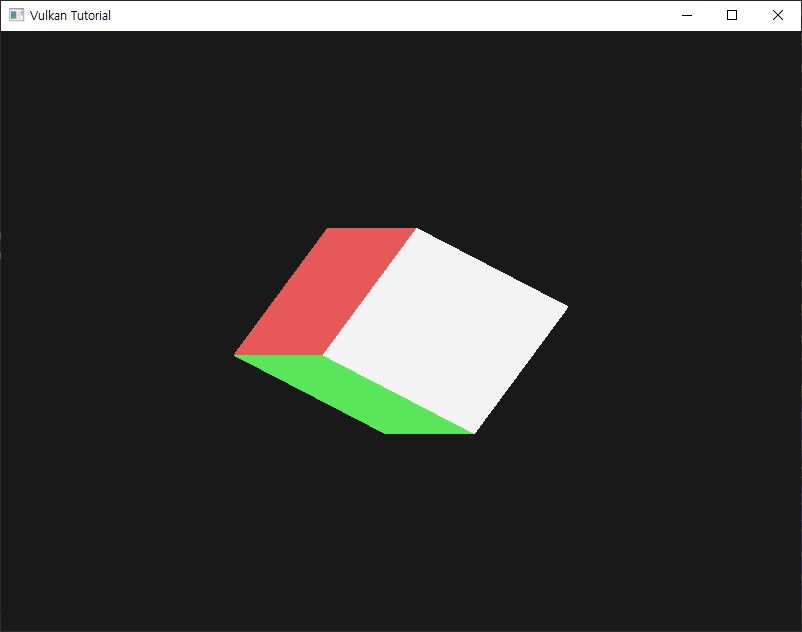
3.6. 실행 결과

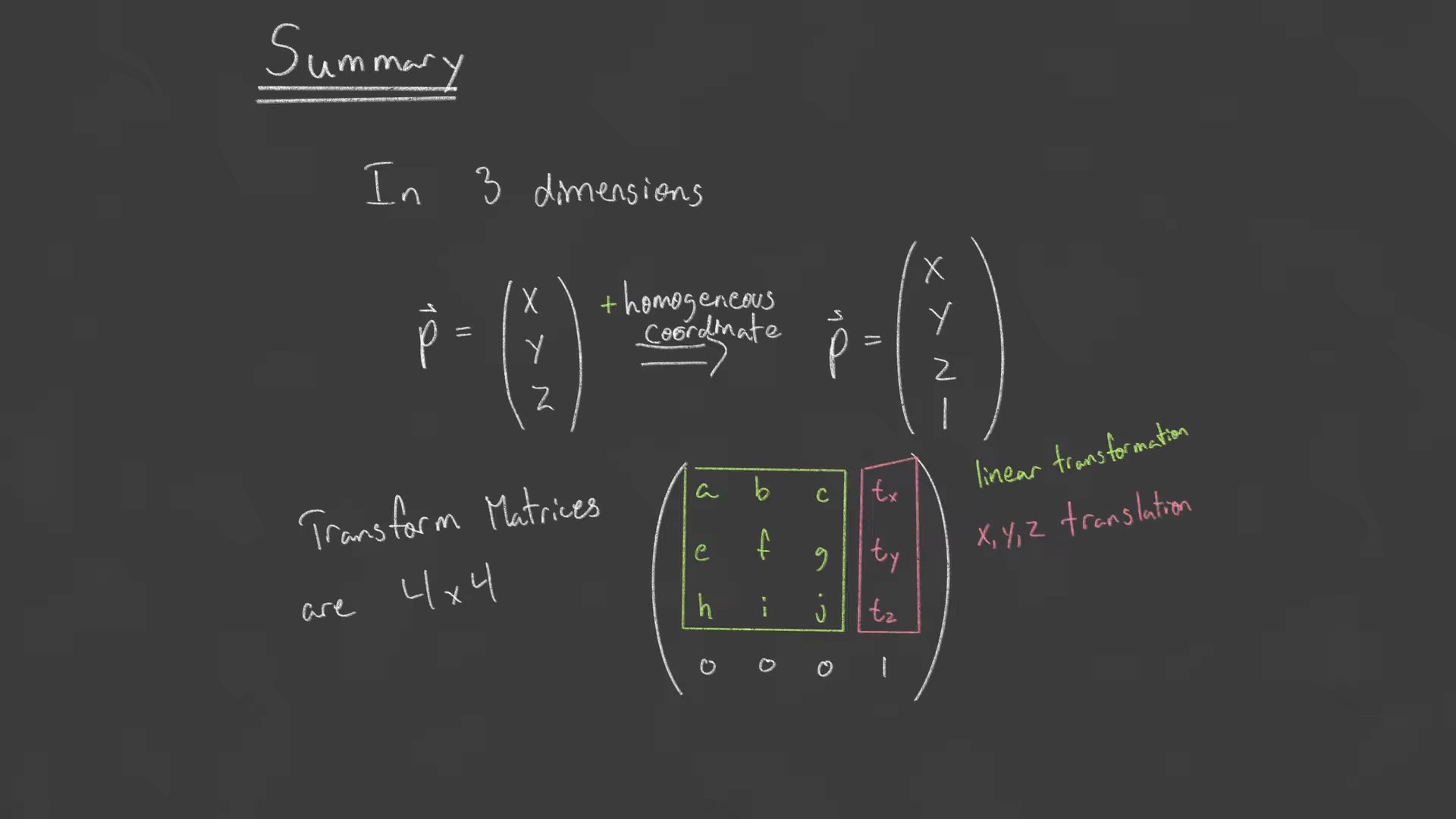
4. Summary

• 점 (x, y, z) 는 (x, y, z, 1) 로 바꿔서 사용합니다.
• 위의 4x4 매트릭스에서, 녹색 3x3 부분은 rotation과 scale을 나타내고, 빨간색 부분은 translation을 나타냅니다.

• 점은 마지막 컴포넌트로 1을 사용하고, 벡터는 0을 사용합니다.
• 3차원에서 회전은 여러 방식으로 나타낼 수 있습니다.